如何理解FOC和SVPWM技术

期末考试结束，RoboGame的各种任务又接踵而至。 在电机的驱动方面，我发现野火的驱动方法不是简单的PWM。 这时，我才学习到，无刷直流电机的控制方法并不是一件简单的事情。

接下来，本人将简单梳理FOC和SVPWM的基础内容。 本文是在互联网学习资源上的个人总结，仅供学习参考和备忘。有疑问处可以查找更加详细的资料。

基础知识

FOC 简介

FOC，Field Oriented Control，是目前无刷直流电机(BLDC)和永磁同步电机(PMSM)高效 控制的最优方法之一。 FOC旨在通过精确地控制磁场大小与方向，使得电机的运动转矩平稳、噪声小、效率高，并且具有高速的动态响应。

FOC具有如下优势：

• 低转速下控制
  由于控制原理的区别，无刷电调只能控制电机工作在高转速下，低速下无法控制；而FOC控制器则完全没有这个限制，不论在什么转速下都可以实现精确控制。
• 电机换向
  同上面的理由，由于电调无法反馈转子位置，因此很难实现电机正反转的换向（当然有感电调可以实现）；而FOC驱动器的换向性能极其优秀，最高转速下正反转切换可以非常顺畅；此外FOC还可以以能量回收的形式进行刹车控制。
• 力矩控制
  普通电调都只能控制电机转速，而FOC可以进行电流（力矩）、速度、位置三个闭环控制。
• 噪音
  FOC驱动器的噪音会比电调小很多，原因是普通电调采用方波驱动，而FOC是正弦波。

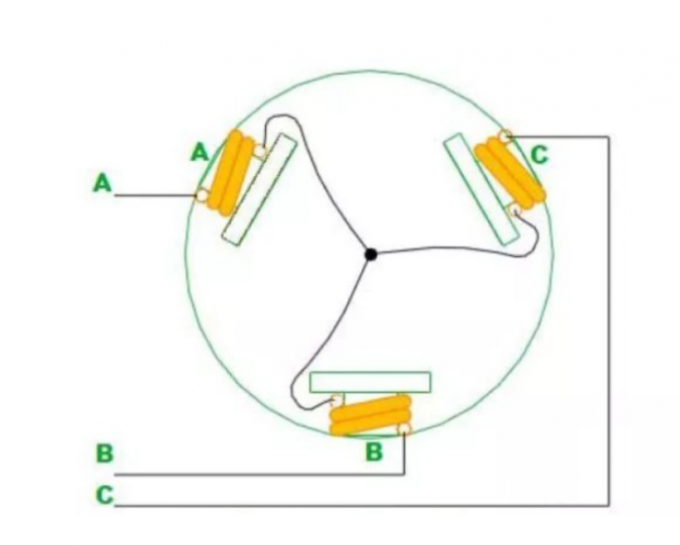
三相星形联结无刷电机

三相星形联结无刷电机中，三相的连接方式是，每一相引出导线的一头，而另一头和其他相两两相连。

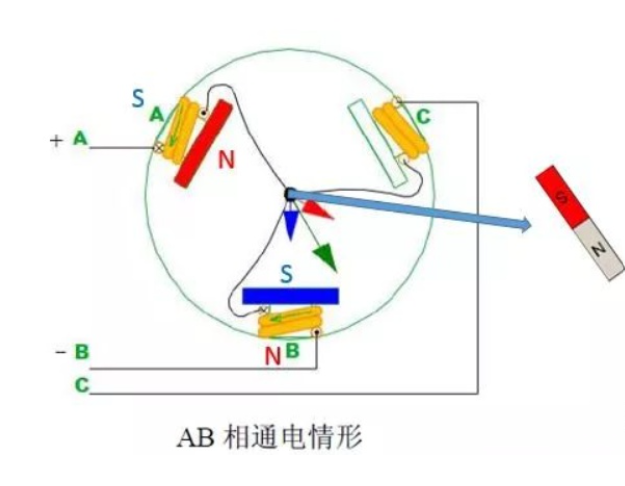
对其中两极施加电压，通过右手螺旋定则和磁感应强度的合成，可以判断线圈磁极的方向。 在这种情况下，转子会倾向于转动到力矩最小的角度，这时转子将会与磁极连线平行， 且磁铁内部磁力线方向和磁极间磁力线方向一致。

因此，无刷电机是通过电子转向来驱动转子不停地转动，换向的频率决定了电机的转速。

BLDC和PMSM

无刷电机其实可以分为无刷直流电机（BLDC）和永磁同步电机（PMSM），结构大同小异，主要区别在于制造方式（线圈绕组方式）不同导致的一些特性差异（比如反电动势的波形）。

BLDC是从硬件出发，采用方波驱动，增加了电机槽和极对数，降低了转子转动的“颗粒感”，达到了平滑驱动的目的。

PMSM是从软件出发，抛弃了方波，而是使用正弦波来完成驱动的平滑化。自然在产生良好特性的正弦波、旋转磁场的同时，会大大
增加驱动器、控制算法的复杂程度。好在野火有例程（

驱动电路

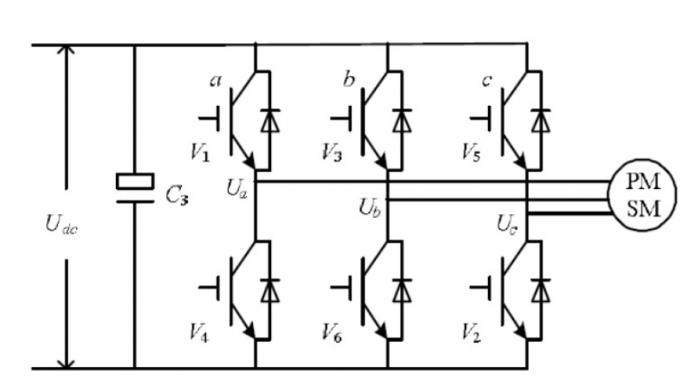
无刷电机的驱动电力主要使用三相逆变电路实现。

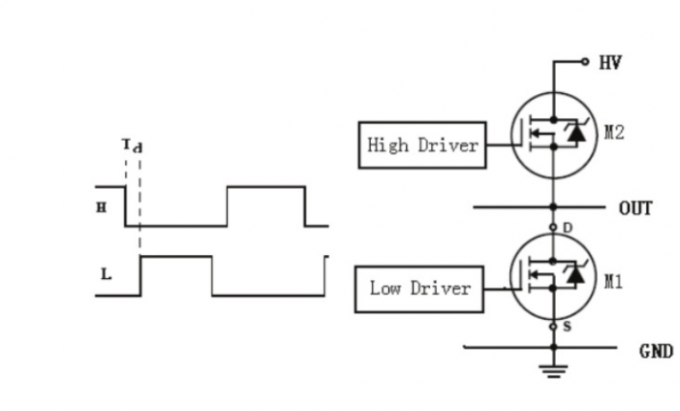
逆变电路是指，将直流电变换为交流电的电路。 逆变电路的具体实现通常是半路MOS电路，原型很简单， 由两个MOS管组成上桥臂和下桥臂，中间引出输出线即可。

用3个半桥电路就可以组合成三相逆变电路，每个半桥引出的一根输出线跟无刷电机的一根相线相连，就完成了最基本的无刷驱动电路。

值得注意的是，原作者在这里提醒到，半桥上下同时导通，则电源短路；同时关闭，则产生了力矩浪费。所以通常半桥工作时，上下两桥臂有且仅有一个导通。

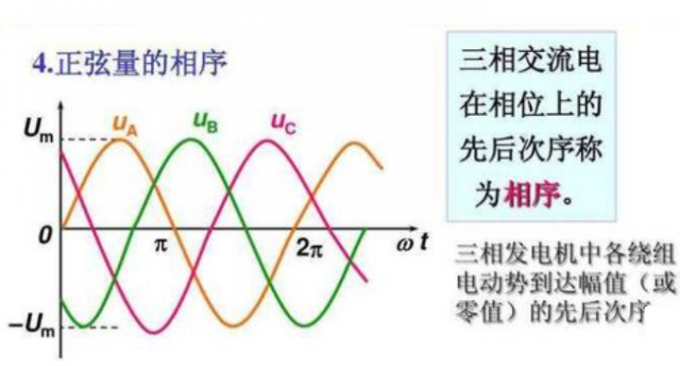
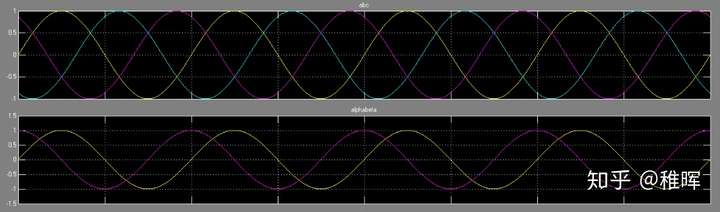
三相电机波形

手动转动无刷电机的转子，利用示波器观察它的三相输出电压，可以得到三根正弦曲线，两两相位差为$120^{\text{o}}$。

相反地，在三相无刷电机的三相线圈上输入这样的三相正弦电压，就可以驱动无刷电机平稳旋转。

于此，可以提出FOC主要驱动手段，即计算所需电压矢量，利用SVPWM技术产生调试信号，驱动三相逆变电路，合成等效的三相正弦电压驱动电机。

FOC控制原理

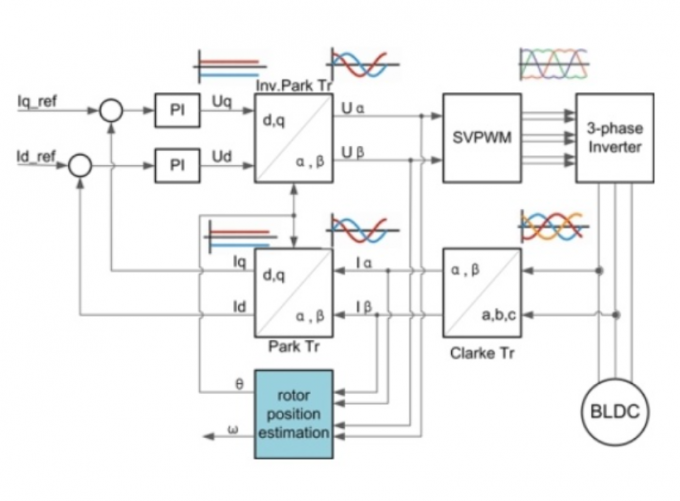
一个基本的FOC控制流程如下所示。

该流程的作用是，利用输入的$I_q $_$ref$和$I_d $_$ ref$，使电机始终产生一个恒定的力矩。

控制流程为

1. 对电机三相电流进行采样得到$I_a, I_b, I_c$。
2. 将$I_a, I_b, I_c$经过 Clark变换得到$I_{\alpha}, I_{\beta}$。
3. 将$I_{\alpha}, I_{\beta}$经过Park变换得到$I_q, I_d$。
4. 计算$I_q, I_d$和其设定值$I_q$_$ref$ $I_d $_$ ref$的误差。
5. 将误差输入PID控制器，得到输出的控制电压$U_q, U_d$。
6. 将$U_q, U_d$进行 反Park变换 得到$U_{\alpha}, U_{\beta}$。
7. 用$U_{\alpha}, U_{\beta}$合成电压空间矢量，输入SVPWM模块进行调制，输出此时刻三个半桥的状态编码值。
8. 按照状态编码值控制三相逆变器的MOS开关，驱动电机。
9. 循环以上步骤。

Clark变换

首先需要对电机的三个相电流进行采用。

根据基尔霍夫定律(KCL)，在任一时刻，流入节点的电流之和等于流出节点的电流之和，也就是说

$$I_a + I_b + I_c = 0$$

因此，三相电流事实上只需要两相即可确定。

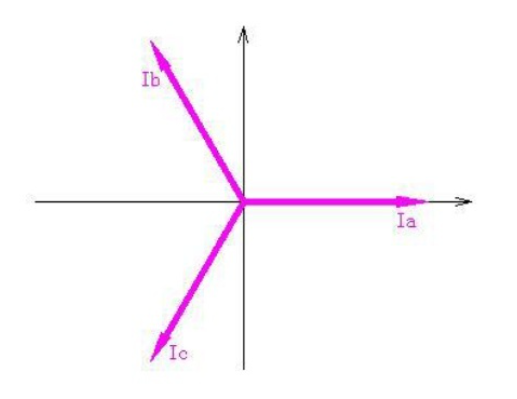
三相坐标系$(I_a, I_b, I_c)$如下。

利用线性代数中的基变换，我们将三相电流转换为直角坐标系下的参量。令新的直角坐标系为$\alpha - \beta$坐标系。

$$\begin{cases} I_\alpha = I_a - \cos (\frac{\pi}{3})I_b - \cos (\frac{2\pi}{3})I_c \\ I_\beta = \sin (\frac{\pi}{3})I_b - \sin(\frac{\pi}{3})I_c \end{cases}$$

或表示为矩阵形式

$$\begin{pmatrix} I_\alpha \\ I_\beta \\ \end{pmatrix} = \begin{pmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{pmatrix} \begin{pmatrix} I_a \\ I_b \\ I_c \end{pmatrix}$$

便可以减少一维变量。

Park变换

Park变换可以将$I_{\alpha}, I_{\beta}$ 转换为线性的。工作原理依然是线性代数原理，即将$\alpha - \beta$坐标系旋转$\theta$角度，其中$\theta$是转子当前的角度。

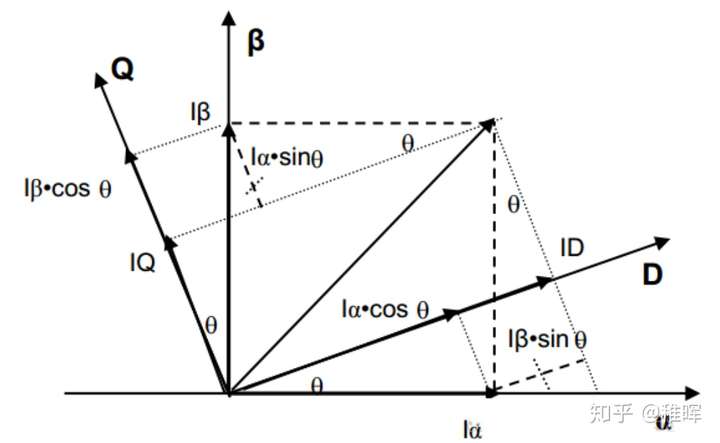
变换公式如下

$$\begin{cases} I_d = I_\alpha \cos (\theta) + I_\beta \sin(\theta) \\ I_q = -I_\alpha \sin(\theta) + I_\beta \cos(\theta) \end{cases}$$

或者为矩阵形式

$$\begin{pmatrix} I_d \\ I_q \end{pmatrix} = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} I_\alpha \\ I_\beta \end{pmatrix}$$

其中$\theta$的获取，需要编码器实时输入转子的实时旋转角度。经过Park变换，一个匀速旋转的向量被转化成了一个定值，两个控制变量也被线性化了。

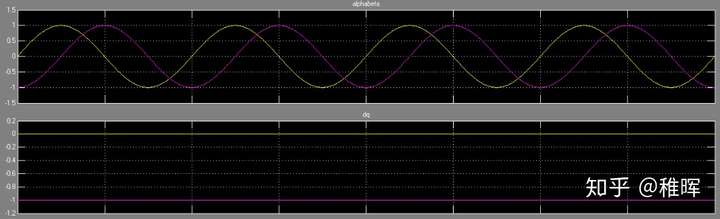
接下里以$I_q, I_d$两个值作为反馈控制的对象，可以用一些线性控制器来进行控制。工业界偏爱PID（

PID 控制

FOC控制中主要使用三个PID环，分别是电流环、速度环和位置环。

具体流程为通过电流反馈控制电机电流（扭矩） -> 通过控制扭矩来控制电机的转速 -> 通过控制电机ed转速控制电机位置。

电流控制环

电流环具有如下控制框图。

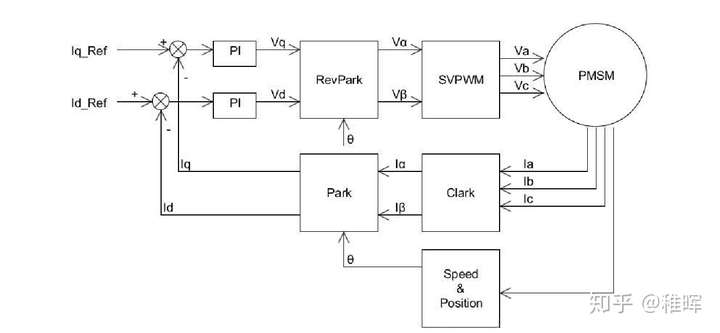
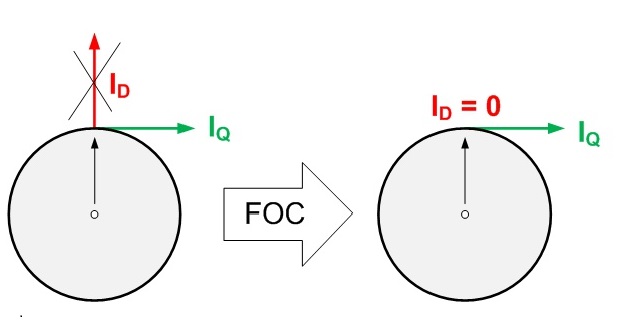
其中的$I_q， I_d$的物理意义如下。

• $I_d$ 为转子旋转的切向变量，是期望的力矩输出。
• $I_q$ 为转子旋转的径向变量，是不期望的力矩输出，期望值为0

事实上，Clark变换 和 Park变换将转子磁链解耦成了转子旋转的径向和切向两个方向的变量。

我们希望通过PID控制器，利用上述输入（电流采样，编码器反馈）和输出（MOS管开关状态）完成对电机电流的闭环控制。

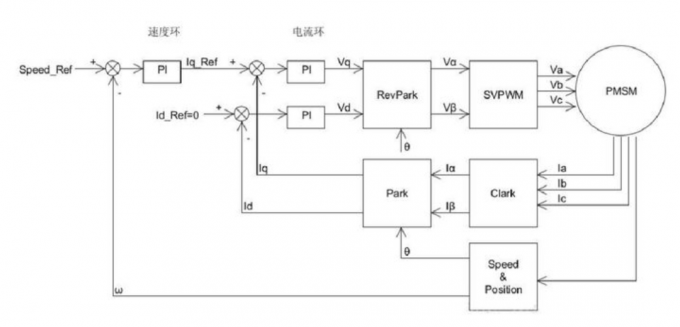
速度控制环

在电流环的外部嵌套速度环，即可获得速度-电流双环控制。

$Speed_{ref}$ 是速度设定值，$\omega$是电机的转速反馈，可以通过电机编码器或者霍尔传感器计算得到。
将电机速度$\omega$和速度设定值$Speed_{ref}$进行误差值计算，带入速度环PI，计算的结果作为电流环的输入，就实现了速度-电流的双闭环控制。

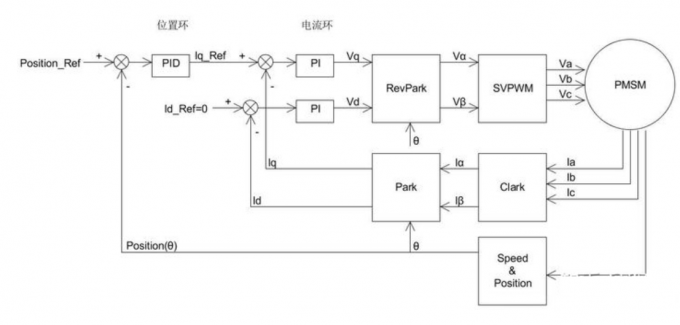
位置控制环

在电流环外部嵌套位置环，即可获得位置-电流双环控制。

由于不存在速度环，这里位置环使用了完整的PID控制。具体原因是，位置的微分是速度，德阳可以减小位置控制的震荡，加快收敛；积分项可以消除静态误差。

空间电压矢量和SVPWM

空间电压矢量

SVPWM的目的，是使用三相桥的开关状态把在空间中旋转的矢量表示出来，这个矢量被称为空间电压矢量。

对于三项桥的任意一种状态，利用数学工具，我们可以计算出三项桥产生的电压矢量$\vec{U}$具有特定的幅值，即相电压峰值$U_{dc}$。这个电压矢量应当具有$\omega=2\pi f$的角速度，才能满足旋转的需要。

使用数学公式

$$\begin{cases} U_A(t) = U_{dc}\cos(2\pi f t) \\ U_B(t) = U_{dc}\cos(2\pi ft - \frac{2\pi}{3}) \\ U_C(t) = U_{dc}\cos(2\pi ft + \frac{2\pi}{3}) \end{cases}$$

定义开关函数$S_x(x\in a, b, c)$。

$$S_x = \begin{cases} 1, & \text{上桥臂导通} \\ 0, & \text{下桥臂导通} \end{cases}$$

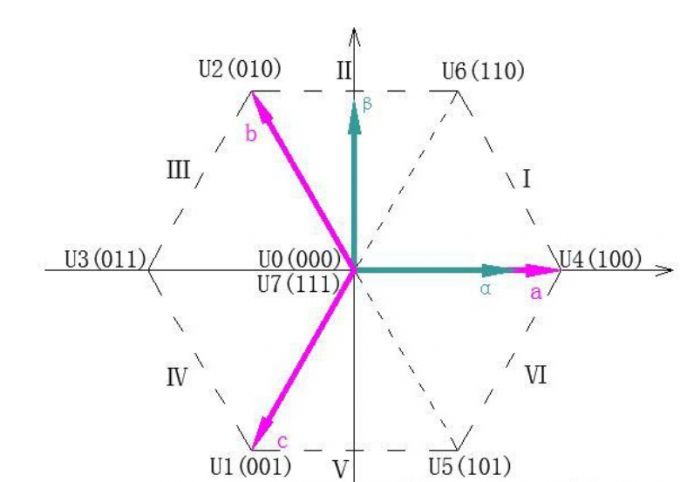
$(S_a, S_b, S_c)$的全部可能组合共有8中，其中有6个非零矢量

$$U_1(001),U_2(010),U_3(011),U_4(100),U_5(101),U_6(110)$$

和两个零矢量

$$U_0(000), U_7(111)$$

可以绘制出各矢量的图像。

SVPWM技术

利用这6个空间电压矢量作为基向量，可以合成任意矢量。在每一个扇区，选取相邻的两个电压矢量以及零矢量，按照伏秒平衡原则来合成每个扇区内的任意电压矢量，即：

$$\int^T_0 U_{ref}\text{d}t = \int^{T_x}_0 U_x\text{d}t + \int^{T_x + T_y}_{T_x} U_y\text{d}t + \int^{T}_{T_x+T_y} U_0^{*}\text{d}t$$

离散化获得公式

$$U_{ref}\cdot T = U_x \cdot T_x + U_y \cdot T_y + U_0^{*} \cdot T_0^{*}$$

其中$U_{ref}$是我们期望的电压矢量，T是一个PWM周期。

$U_x, U_y$的选取，应当是$U_{ref}$所在扇区的两侧。

$U_0^{*}$指的是两个零矢量，可以是$U_0$或者$U_7$，零矢量的选择比较灵活，通过合理地配置零向量可以让空间电压矢量的切换更平缓。

因此，只需要周期性的切换不同空间电压矢量，合理配置不同基向量在一个周期中的占空比，就可以合成出等效的任意空间电压矢量。

七段式SVPWM调制法

七段式SVPWM是指，合理安排SVPWM中的各空间矢量的占空位置，使得MOS管的开关次数最小，最大限度地减少开关损耗的一种调制思路。

依照$U_{ref}$的所在扇区，可以计算得到如下开关切换顺序

$U_{ref}$ 所在扇区	开关切换顺序
Ⅰ区	$…0-4-6-7-7-6-4-0…$
Ⅱ区	$…0-2-6-7-7-6-2-0…$
Ⅲ区	$…0-2-3-7-7-3-2-0…$
Ⅳ区	$…0-1-3-7-7-3-1-0…$
Ⅴ区	$…0-1-5-7-7-5-1-0…$
Ⅵ区	$…0-4-5-7-7-5-4-0…$

至此，SVPWM的任务完成，只需要在处理器中赋值给对应通道的捕获比较寄存器产生相应的三个PWM波形，控制MOS管的开关，进而产生期望的电压、电流和力矩。

总结

“矢量控制”事实上是一种解耦合，把相互耦合的三相磁链解耦为容易控制的两轴$I_q$和$I_d$，计算得到响应结果后，再将控制信号耦合传回电机。